С приходом компьютеров и развитием вычислительных мощностей в нашу жизнь, у некоторых людей стали появляться тревоги относительно своего будущего. «Если роботы могут считать быстрее людей, и мы научим их распознавать эмоции, не заменят ли они нас окончательно?» Но в эти быстро меняющиеся времена наука еще больше доказывает, что сила человеческого мозга непобедима, особенно когда у нее есть такой сильный союзник, как компьютер. И относительно новый раздел моделирования – теория сложных систем – это подтверждает.
О теории
Наука о сложных системах – это область на стыке математики, информатики и естествознания, которая фокусируется на сложных системах, представляющих собой системы со множеством взаимодействующих компонентов.
Такие модели используются в естественных и общественных науках, а иногда в искусстве и гуманитарных науках.
Меняющиеся критерии науки
Наука о сложных системах – это не просто другой набор моделей; это также постепенное изменение критериев, по которым оцениваются модели, и типов моделей, которые считаются «научными». Например, классические модели, как правило, основаны на законах физики, выражаются в форме уравнений и решаются с помощью математического вывода. Модели же, попадающие в зону поведения сложных систем, часто основаны на правилах, описании, выражаются в виде вычислений, словесных формулировок и моделируются, а не анализируются.
Наука о сложных системах находится в центре медленного сдвига в научной деятельности и изменения того, что мы считаем наукой и многие нобелевские лауреаты используют этот инструментарий при моделировании экономических и социальных процессов. Ее новизна состоит не в том, что она применяет инструменты науки к новому предмету, как часто бывает в диссертационных исследованиях фундаментальных наук, а в том, что использует разные инструменты, допускает различные виды работы и в конечном итоге меняет то, что мы подразумеваем под словом «наука», создавая простые модели со сложным поведением благодаря компьютерам.
На пальцах
Аллен Б. Дауни – профессор информатики в колледже имени Франклина В. Олина в своей книге «Изучение сложных систем с помощью Python» приводит такой пример.
Предположим, кто-то спрашивает вас, почему планетарные орбиты эллиптические. Пользуясь основами классической науки, вы можете вызвать закон всемирного тяготения Ньютона и использовать его для написания дифференциального уравнения, которое описывает движение планет. Затем вы можете решить дифференциальное уравнение и показать, что решение является эллипсом. Что и требовалось доказать! Большинство людей находит такое объяснение удовлетворительным. Оно включает в себя математический вывод – так что оно имеет некоторую строгость доказательства – и объясняет конкретное наблюдение, эллиптические орбиты, ссылаясь на общий принцип, гравитацию.
Теперь сопоставим это с другим типом объяснения. Предположим, вы переезжаете в такой город, как Детройт, в котором существует расовая сегрегация, и хотите знать, почему это так. Если вы проведете исследование, то можете найти статью нобелевского лауреата Томаса Шеллинга «Динамические модели сегрегации», в которой предлагается простая модель расовой сегрегации.
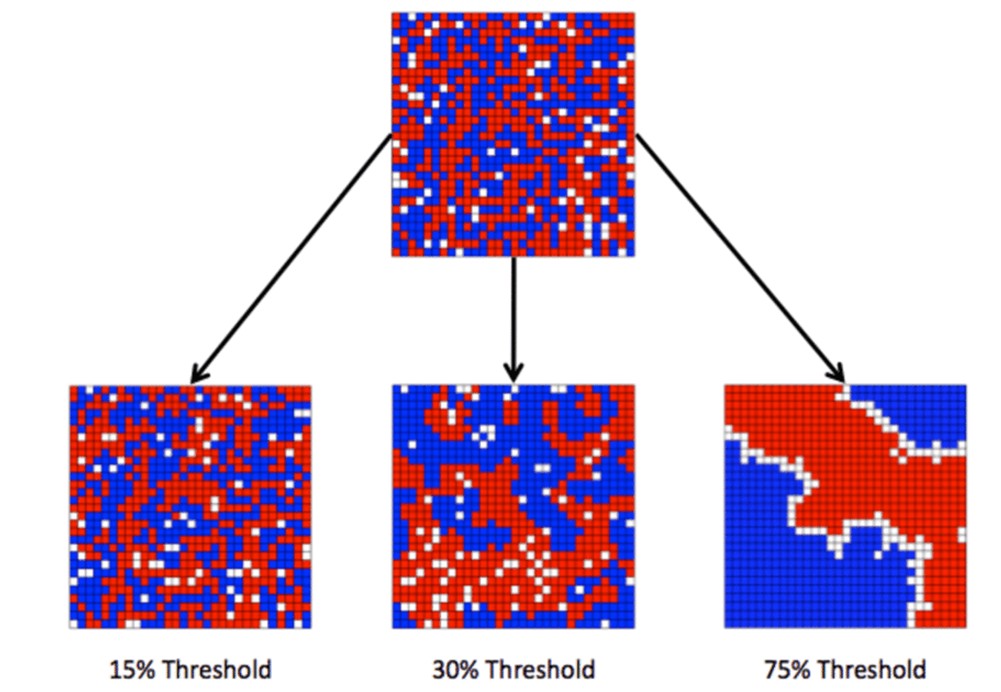
Модель города Шеллинга представляет собой массив ячеек, где каждая ячейка представляет собой дом. Дома заняты двумя типами «агентов», обозначенных красным и синим, в примерно равных количествах. Около 10 % домов пусты. В любой момент времени агент может быть счастлив или несчастен, в зависимости от других агентов по соседству. В одной версии модели агенты счастливы, если у них есть как минимум два соседа, таких как они, и недовольны, если у них есть один сосед или ноль соседей. Симуляция продолжается, выбирая агента наугад и проверяя, счастлив ли он. Если это так, ничего не происходит; если нет, агент случайным образом выбирает одну из незанятых ячеек и переезжает. Если вы начнете со смоделированного города, который полностью несегрегирован, и запустите модель на короткое время, появятся кластеры похожих агентов. Со временем кластеры растут и сливаются, пока не образуется небольшое количество крупных кластеров, и большинство агентов не живет в однородных окрестностях.
Степень сегрегации в модели удивительна, и это предлагает объяснение сегрегации в реальных городах. Может быть, Детройт сегрегирован, потому что люди предпочитают не быть в меньшинстве и будут двигаться, если состав их окрестностей делает их несчастными. Является ли данное объяснение удовлетворительным так же, как и в случае с объяснением движения планет? Многие математики скажут, что нет. Почему?
Очевидно, что модель Шеллинга очень абстрактна, то есть не реалистична. Таким образом, у вас может возникнуть соблазн сказать, что люди сложнее, чем планеты. Но это не может быть правдой. В конце концов, на некоторых планетах есть люди, поэтому они должны быть сложнее, чем люди. Обе системы сложны, и обе модели основаны на упрощениях. Например, в модели движения планет мы включаем силы между планетой и ее солнцем и игнорируем взаимодействия между планетами. В модель Шеллинга мы включаем индивидуальные решения, основанные на местной информации, и игнорируем все остальные аспекты человеческого поведения. Но есть различия в степени. Что касается движения планет, мы можем защитить модель, показав, что игнорируемые нами силы меньше, чем те, которые мы включаем. И мы можем расширить модель, чтобы включить другие взаимодействия и показать, что эффект невелик. Что касается модели Шеллинга, то здесь сложнее обосновать упрощения.
Еще одно отличие состоит в том, что модель Шеллинга не обращается к каким-либо физическим законам и использует только простые вычисления, а не математический вывод. Такие модели, как модель Шеллинга, не похожи на классическую науку, и многие люди находят их менее убедительными, по крайней мере вначале. Но эти модели выполняют полезную работу, в том числе предсказание, объяснение и проектирование.
Выводы
Почему вам следует знать о науке сложных систем? Вот несколько причин:
- наука о сложных системах полезна, особенно если необходимо объяснить поведение природных и социальных систем. Начиная с Ньютона, математическая физика была сосредоточена на системах с небольшим количеством компонентов и простыми взаимодействиями. Эти модели эффективны для некоторых приложений, таких как небесная механика, и менее полезны для других, таких как экономика. Наука о сложных системах обеспечивает разнообразный и адаптируемый инструментарий моделирования;
- множество основных результатов науки о сложных системах удивительно; тема, состоит в том, что поведение простых моделей может быть сложным, а следствием этого является то, что иногда можно объяснить сложное поведение в реальном мире, используя простые модели;
- изучение науки о сложных системах дает возможность узнать о разнообразных физических и социальных системах, развить и применить навыки программирования и поразмыслить над фундаментальными вопросами философии науки.
Все вышесказанное лишний раз показывает, что современные науки сильно нуждаются в тесном сотрудничестве наших интеллектуальных возможностей и компьютера, так как модели сложных систем часто основаны на простых правилах и реализуются в виде вычислений, которые не имеют значения без экспертной интерпретации.
Текст: Алевтина Шаталова, преподаватель Факультета информационных технологий и анализа больших данных Финансового университета, лектор и автор курсов GeekBrains (Mail.ru)
| Комментарии: |